What is Beer-Lambert Law?

• The Beer-Lambert Law, also known as Beer’s Law or the Lambert-Beer Law, is a fundamental principle in analytical chemistry that relates the attenuation of light to the properties of a material through which the light passes. When a monochromatic light of initial intensity (Io) travels through a transparent vessel containing a solution, some of the light is absorbed, resulting in a decrease in the intensity of the transmitted light (I).
• The attenuation of light can occur due to various factors such as scattering by particles in the solution, reflection at interfaces, and most significantly, absorption by the solution itself. The relationship between the transmitted light intensity (I) and the initial light intensity (Io) depends on two key factors: the path length (l) of the absorbing medium and the concentration (c) of the absorbing solution. These factors are precisely described by the laws of Lambert and Beer.
• The Beer-Lambert Law states that the energy absorbed or transmitted by a solution is directly proportional to the molar absorptivity of the solution and the concentration of the solute. This law is widely used in analytical chemistry to measure the absorbance of various samples. It combines the principles of Beer’s Law and Lambert’s Law to provide a comprehensive understanding of light attenuation through a substance and its related properties.
• The application of the Beer-Lambert Law spans across various fields, including pharmaceutics and organic chemistry analysis. It elucidates the direct relationship between the path length and concentration of a sample being studied and the absorbance of the incident light ray. By utilizing this law, scientists and analysts can determine the concentration of a solute in a solution by measuring its absorbance.
• August Beer was the first to state the Lambert-Beer Law, which is mathematically expressed as I = Ioe^(-μx), where I represents the transmitted light intensity, Io is the initial light intensity, μ is the molar absorptivity coefficient, and x is the path length through the absorbing medium.
• In summary, the Beer-Lambert Law is a fundamental principle that explains the relationship between the attenuation of light passing through a substance and the properties of that substance. It finds broad application in analytical chemistry, allowing scientists to measure the absorbance of samples and determine the concentration of solutes in solutions.

Beer-Lambert Law

Beer-Lambert law states that- 

The absorbance of a solution is proportional to its concentration, molar absorption coefficient, and optical coefficient.

• Beer’s Law, often known as Beer’s Law or the Beer-Lambert-Bouguer law, states the relationship between a solution’s absorbance and its concentration, molar absorption coefficient, and optical coefficient.
• When monochromatic light flows through a homogeneous media, the intensity of the transmitted radiation drops at a constant rate as the medium thickness rises. This drop in intensity is proportional to the solution concentration. In other words, as the concentration of the solution increases, so does the absorption of the transmitted light.
• The Beer-Lambert Law defines a linear connection between a solution’s absorbance and concentration. Based on the absorbance of a solution, scientists and analysts can compute its concentration. The concentration of a solute in a solution may be determined by measuring the absorbance of a sample and knowing the molar absorption coefficient.
• The law also states that the absorption of light by a material dissolved in a completely transmitting solvent is exactly proportional to the substance’s concentration and the light’s journey length through the solution. The absorption spectrum will have a larger peak intensity when more molecules in the solution absorb light of a specific wavelength. If fewer molecules absorb the radiation, the overall amount of energy absorbed is lowered, resulting in a lower intensity peak.
• Several scientists are credited with discovering the Beer-Lambert Law. In 1729, Pierre Bouguer developed the rule, and in 1760, Johann Heinrich Lambert observed that the absorbance of a sample is related to the light path length. In 1852, August Beer developed a matching rule stating that absorbance is proportional to sample concentration.
• In conclusion, the Beer-Lambert Law is an important concept in spectroscopy and analytical chemistry. It establishes the link between a solution’s absorbance and its concentration, as well as the molar absorption coefficient and optical coefficient. This rule allows scientists to use absorbance to calculate the concentration of a solute in a solution, making it a useful tool in a variety of scientific areas.

What is the Beer-Lambert Law?

The Beer-Lambert law is a linquisimal relation between the absorbance, the concentration of the solution, its molar absorption coefficient, and the optical coefficient in a solution.

A = εLc

Where,

• A is the amount of light absorbed for a particular wavelength by the sample
• ε is the molar extinction coefficient
• L is the distance covered by the light through the solution
• c is the concentration of the absorbing species

The absorption coefficient of molar is a property that depends on the sample that measures how powerful an absorber the sample is when it comes to the wavelength at which it is. The concentration is one mole (M) in the solution of the material dissolving in the solution. it is measured by the length of the cuvette that is used to measure absorbance, which typically is 1 centimeter.

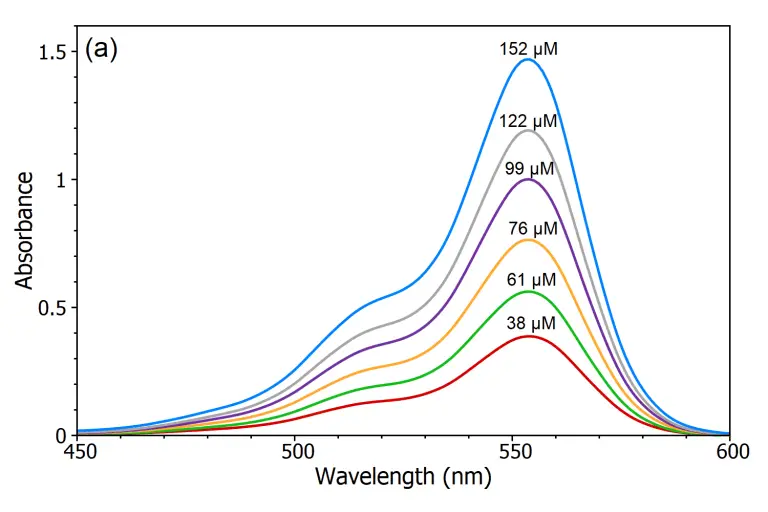
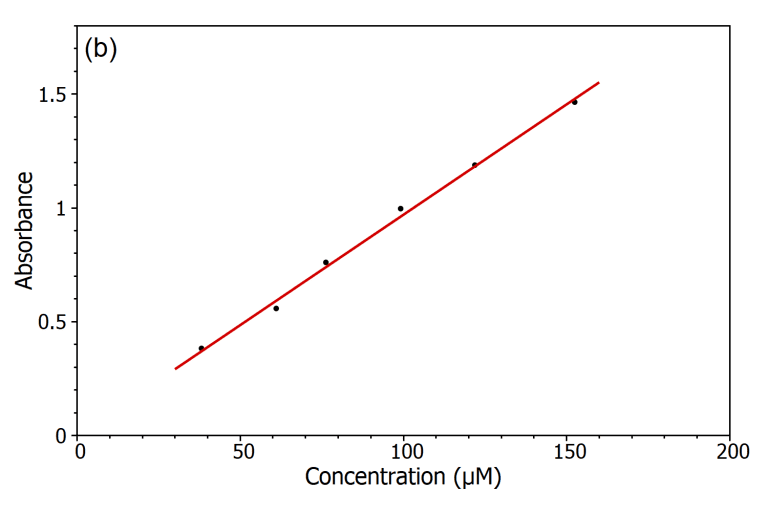
The Beer-Lambert law declares the existence of a linear relation between the amount of solution and its absorbance that allows that the amount of substance to be determined by taking the measurement of its absorbance. To show this linear dependence, the absorbance of five different solution solutions for Rhodamine B in water were determined by using the DS5 Dual Beam Spectrophotometer (Figure a) and from the absorption spectra, an linear calibration curve for the absorption versus the concentration was drawn (Figure b). By using this calibration curve, to determine the amount of an unidentified Rhodamine B solution can be measured by measuring its absorbance which is the primary purpose in this law. Beer-Lambert Law.

Beer lambert law equation

Beer’s Law may be written simply as:

A = εbc

• where A is absorbance (no units)
• ε is the molar absorptivity with units of L mol-1 cm-1 (formerly called the extinction coefficient)
• b is the path length of the sample, usually expressed in cm
• c is the concentration of the compound in solution, expressed in mol L-1

The method of calculating the absorbance of a sample by using the equation is based upon two conditions:

• It is proportional directly to in the length of the cuvette (the length of cuvette).
• It is proportional directly to the amount of the substance.

Beer-Lambert Law Formula

The Beer-Lambert law equation is as follows:

I = I₀e^-μ(x)

Where,

• I is the intensity
• I0 is the initial intensity
• μ is the coefficient of absorption
• x is the depth in meter

How to derive the Beer-Lambert Law equation? (Derivation of Beer Lambert Law) – Derivation of Beer-Lambert Law

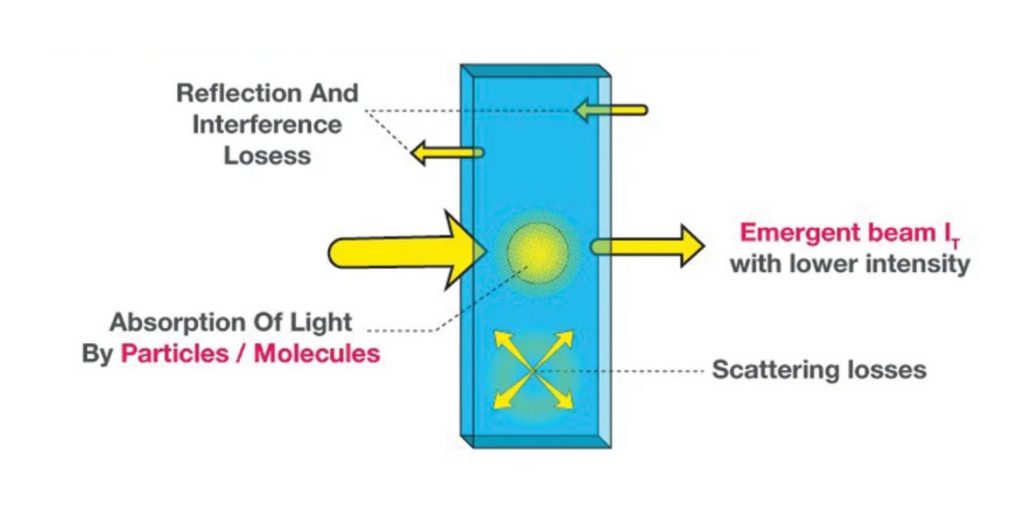
Absorption of energy causes the absorption of light as well usually by electrons. Different forms of light such as visible light and ultraviolet light get absorbed in this process. Therefore, change in the intensity of light due to absorption, interference, and scattering leads to:

ΔI = I0 – IT

The following equations are necessary for us to obtain our ultimate derivative equation. Transmittance is measured as the ratio of light passing through a substance. It can be calculated as IT/I0. To calculate the of transmittance percentage we can do so by:

%T = 100I_r/I₀

Percent Transmittance Another key metric is absorbance that is defined as the amount of light absorbed. This is usually calculated as the negative of transmittance and is given by:

A = log₁₀ I₀/I_T=log₁₀(1/T)= – logT = 2 – log (%T)

Absorbance (A) The rate of decrease in the intensity of light with the thickness of the material the light is directly proportional to the intensity of the incident light. Mathematically, it can be expressed as:

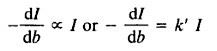
As k’= Proportionality constant

Taking in the reciprocal of the equation we get,

-dl/db = 1/K’l

Integrating the above equation we also get,

-b = 1/k’ InIr + C

In the above equation, b and C is the constant of integration and IT is the intensity being transmitted at the thickness

In order to solve the above equation with the constant of integration, we then get,

C = – 1/K’ InI₀

While solving for C in the equation will give us,

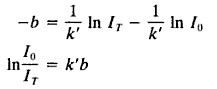
Converting to log10 we get,

logI₀/I_r = K’b/2.303

Rearranging the equation we get,  A = K’b/2.303

So, Lambert’s law was created and declares that the monochromatic radiation increases exponentially and decreases as it is passed through a medium with a uniform thickness.

log I₀/I_r = K”c/2.303 or A = K”c/2.303

This concludes the Beer-Lambert law’s derivation. This demonstrates that, in order to create an exact law there are lots of equations that have to be figured out before achieving the desired outcome.

Beer lambert law calculator

• https://www.omnicalculator.com/chemistry/beer-lambert-law
• https://www.aatbio.com/tools/quick-calculator/beer-lambert-formula-calculator
• https://www.sigmaaldrich.com/IN/en/support/calculators-and-apps/absorbance-transmittance-conversion
• https://www.calculatorhut.com/chemistry/beer-lambert-law.html
• http://calistry.org/calculate/beerLambertLawAbsorbance
• https://byjus.com/beer-lambert-law-calculator/

Beer-Lambert Law Example Calculation

Q1. Determine the relative amount of light that is absorbed by the sample if the absorbance of the sample is 1 at a specific wavelength.

According to the definition of absorbance;

A = log₁₀ (I₀/I)

The equation is rearranged to determine the relative loss of intensity

10A = I₀/I

10-A= I/I₀

Substituting the value of A = 1

1-I/I₀ = 1 – 10-1 = 1 – 1/10 = 0.9

Therefore, we can say that 90% of the light is absorbed and 10% of light is transmitted.

Q2. Cytosine has a molar extinction coefficient of 6*103 at 270 nm at pH 7. Calculate the absorbance and percent transmission of 1*10-4 and 1*10-3 M cytosine solution in a 1-mm cell. 

Solution

For 1*10^-4M, the absorbance A is given as,

A = log(I₀/I) = e * b * c = 6*10³ * 0.1 * 1*10^-4 = 0.06

in percent transmission, I/I₀ * 100,

A_% = 10^-0.06 * 100 = 10^1.94 (%) = 87.10 %

Similarly, for 1*10^-3M, the absorbance A is given as,

A = log(I₀/I) = e * b * c = 6*10³ * 0.1 * 1*10^-3 = 0.6

in percent transmission, I/I₀ * 100,

A_% = 10^-0.6 * 100 = 10^1.4 (%) = 25.12 %

Q3. A protein with extinction coefficient E1% = 16 yields an absorbance of 0.73 when measured in a 0.5-cm cell. Calculate the weight concentration.

Solution

The absorbance in E^1% can be written as,

A = E^1% * b * c

Where A = 0.73 in a 0.5-cm cell, and = 16. Then, the weight concentration is

c = A / (E^1% * b) = 0.73 / (16*0.5) = 0.091 g/100ml

Q4. Determine the concentration of glycogen-iodine complex if the transmission of light is 40%. Also, the absorption coefficient is 0.20 at 450 nm. The size of the cuvette is 2 cm.

Answer:

Using Beer-Lambert’s law, we know that

-log(It) = -log10(0.4) = (0.20)(c)(2)

c = 0.994

Instrumentation of Beer-Lambert Law

The majority of measurements in experimental research are done using the term transmittance (T) which is described as:

T = I / Io

in which I represents the intensity of light that it reaches after passing through the sample, and Io is the light intensity. The relationship between T and A is:

A = -log T = – log (I / Io).

Absorption of light by a sample;

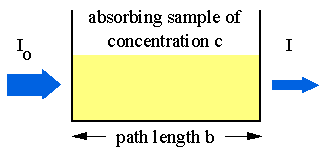
Modern absorption instruments typically display the data in one of three ways: transmittance, %-transmittance or absorbance. A concentration that is not known for an analyte is determined by taking measurements of the quantity of light the sample absorbs, and then employing Beer’s law. If the absorptivity coefficient of the sample is not known, the undetermined concentration can be determined by using the absorption curve against concentration calculated from standards.

Applications of Beer-Lambert Law 

1. Application in Analytical chemistry

This study focuses on its separation and quantification and characterization of matter through the spectrophotometry. It does not require lengthy pre-processing of the sample to obtain the result. For example, the count of bilirubin in blood samples can be measured by using the spectrumrophotometer.

2. Application In atmosphere

The solar or stellar radiation that occurs in the atmospheric layer can be described with this law. The law applicable to atmospheric applications is an altered equation:

T=e^{_−m(Ta_{+Tg+TRS+TNO2+Tw+TO3+Tr+..)}}

Where,

• a is the aerosols
• g is the mixed gases
• RS is the Raman scattering effect.
• NO2 is Nitrogen dioxide
• w is the water vapour absorption
• O3 is Ozone
• r is Rayleigh scattering

Limitations of Beer-Lambert Law 

Linearity in the law of Beer-Lambert is influenced by instrumental and chemical causes. Some of the causes of nonlinearity are

• Absorptivity coefficients are affected by deviations at higher concentrations (>0.01M) because of Electrostatic interactions among molecules that are in close proximity
• scattering of light caused by particles within the sample
• fluoresecence or phosphorescence in the sample
• changes in refractive indexes at the concentration of high analytes
• changes in chemical equilibrium in relation to concentration
• Non-monochromatic radiation are minimized making use of a flat portion of the spectrum, like the highest point in an absorption spectrum
• Lights that are stray

FAQ

Q1. What is the reason Beer’s Law is so important?

Beer’s Law is especially important in the areas of physics, chemistry and meteorology. Beer’s Law is used in Chemistry to assess levels of chemicals, to study the rate of oxidation and to determine the degradation of polymers. The law also explains the absorption of radiation by the atmosphere of Earth. Although it is typically used to describe radiation, it aids scientists in understanding what causes the emission of particles like neutrons. In theoretical physics, the Beer-Lambert Law is a solution to the Bhatnagar-Gross-Krook (BKG) operator, which is used in the Boltzmann equation for computational fluid dynamics.

Q2. How can we make use of Beer’s Law?

Many modern instruments can perform Beer’s Law calculations by simply comparing a blank cuvette to the sample, it’s relatively easy to create graphs with standard methods to calculate the amount of substance present in a sample. The method of graphing is based on a straight line relationship between concentration and absorbance, which is applicable for dilute solutions.

Q3. What’s Beer’s Law?

The law of Beer states that the absorbance and concentration have a direct correlation to one their respective levels. This was declared by August Beer.

Q4. What exactly is Lambert Law?

Lambert law states that absorption and length of the path are directly proportional. This was formulated in the work of Johann Heinrich Lambert.

Q5. Why is it that Beer-Lambert law fail in higher concentrations?

Beer-Lambert law is ineffective at higher concentrations due to the fact that the law’s linearity is restricted to instrumental and chemical factors. If the solution is at higher concentrations, the relationship between the molecules in the solution is such that there is a deviation in absorptivity. Additionally as the solution’s concentration gets high the refractive index is altered.

References

• Dr. Thomas G. Mayerhöfer,Dr. Susanne Pahlow,Prof. Dr. Jürgen Popp, The Bouguer-Beer-Lambert Law: Shining Light on the Obscure,  https://doi.org/10.1002/cphc.202000464
• Beer, August. “”Bestimmung der Absorption des rothen Lichts in farbigen Flüssigkeiten” (Determination of the absorption of red light in colored liquids).” Annalen der Physik und Chemie, vol. 86, 1852, pp. 78–88.
• Bouguer, Pierre. Essai d’optique sur la gradation de la lumière. Claude Jombert, 1729 pp. 16–22.
• Ingle, J. D. J., and S. R. Crouch. Spectrochemical Analysis. Prentice Hall, 1988.
• Lambert, J. H. Photometria sive de mensura et gradibus luminis, colorum et umbrae [Photometry, or, On the measure and gradations of light, colors, and shade]. Augsburg (“Augusta Vindelicorum”). Eberhardt Klett, 1760.
• https://en.wikipedia.org/wiki/Beer%E2%80%93Lambert_law
• https://www.edinst.com/blog/the-beer-lambert-law/
• https://byjus.com/physics/derivation-of-beer-lambert-law/
• http://life.nthu.edu.tw/~labcjw/BioPhyChem/Spectroscopy/beerslaw.htm
• https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Spectroscopy/Electronic_Spectroscopy/Electronic_Spectroscopy_Basics/The_Beer-Lambert_Law
• https://www.bellevuecollege.edu/wp-content/uploads/sites/140/2014/06/161lab_BeersLawUpdatedPSGF-2-4-2016.pdf
• https://www.thoughtco.com/beers-law-definition-and-equation-608172