Table of Contents
Gibbs free energy is also referred to as the Gibbs function. Gibbs energy, also known as free enthalpy, is the measurement used to determine the highest amount of work that can be done in a thermodynamic process when temperatures and pressures remain constant. Gibbs free energy can be identified by the symbol “G”. Its value is typically measured by Joules and Kilojoules. Gibbs free energy could be defined as the largest amount of work that can be taken from the closed system.
This property was discovered by an American researcher Josiah Willard Gibbs in the year 1876, when he was conducting experiments to understand the behavior of different systems when they were combined, or if a particular process could be performed simultaneously and in a spontaneous manner. Gibbs ‘ free energy was before known in the past as “available energy.” It could be described as the amount of useful energy in a thermodynamic system which can be used to accomplish the work.
What is gibbs free energy?
Gibbs Free Energy is the thermodynamic value of a system, which provides the energy needed for work. It’s used to determine if the reaction is spontaneous. Simply put, spontaneous reactions are those that happen naturally in a natural way, while nonspontaneous reactions are those that don’t. What I am referring to by “naturally” is that a reaction can occur in a given system without the net flow of energy that is free from its surroundings. For instance, ice at 10oC or 1atm can melt quickly, while ice at -10oC and 1atm won’t.
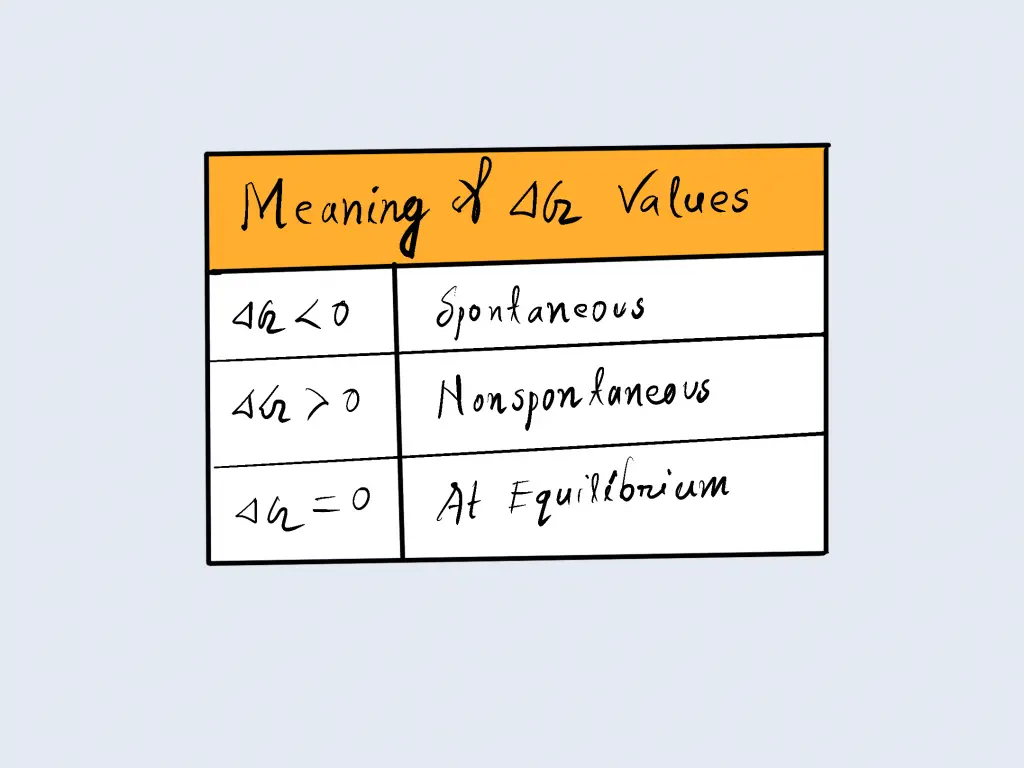
We can see that in a process that is spontaneous, an organism will use up’ a portion of its free energy, and changes in the Gibbs’ free energy can be negative ( ΔG<0) in an unplanned process. The change in Gibbs ‘ free energy can be positive ( ΔG>0) in a non-spontaneous process that will require the input of free energy from the environment. In addition, the increase in Gibbs’ free energy can be counted as negative ( ΔG=0) for the reaction that has reached equilibrium. The results are listed in the table below.
ΔG = ΔH – TΔS
The variation in Gibbs free energy ( ΔG) for any system is dependent on the variation in the enthalpy ( ΔH) along with the changes in the entropy ( ΔS) in accordance with the equation below:
ΔG = ΔH – TΔS
ΔGo = ΔHo – TΔSo
The relation is valid under standard conditions , as well as in non-standard conditions. It is possible to draw few generalizations about the conditions under which a reaction can be spontaneous (i.e. when ΔG<0).
The negative values of ΔH and positive values for ΔS both play a role in achieving a negative value for ΔG and the possibility of a spontaneous reaction. In order for a reaction even be a possibility of being spontaneous, at the very least one of the two (negative ΔH or positive ΔS) must be present.
The primary term that is used in the calculation of ΔG is ΔH which is the enthalpy shift that is the basis for many reactions and conditions, and it is the most dominant element in the equation. This is the reason we frequently expect that the majority of endothermic reactions (negative ΔH) will be spontaneous, while the majority of endothermic reactions (positive ΔH) will not however we are unable to affirm this with absolute certainty.
The second element in formulating ΔG is T ΔS. ΔS tends to be significantly smaller than ΔH which is the reason why ΔH is typically the main element in the equation. However, temperature is also an aspect of this word, and this term, as well as ΔS specifically, plays an increasing significance as temperature increases.
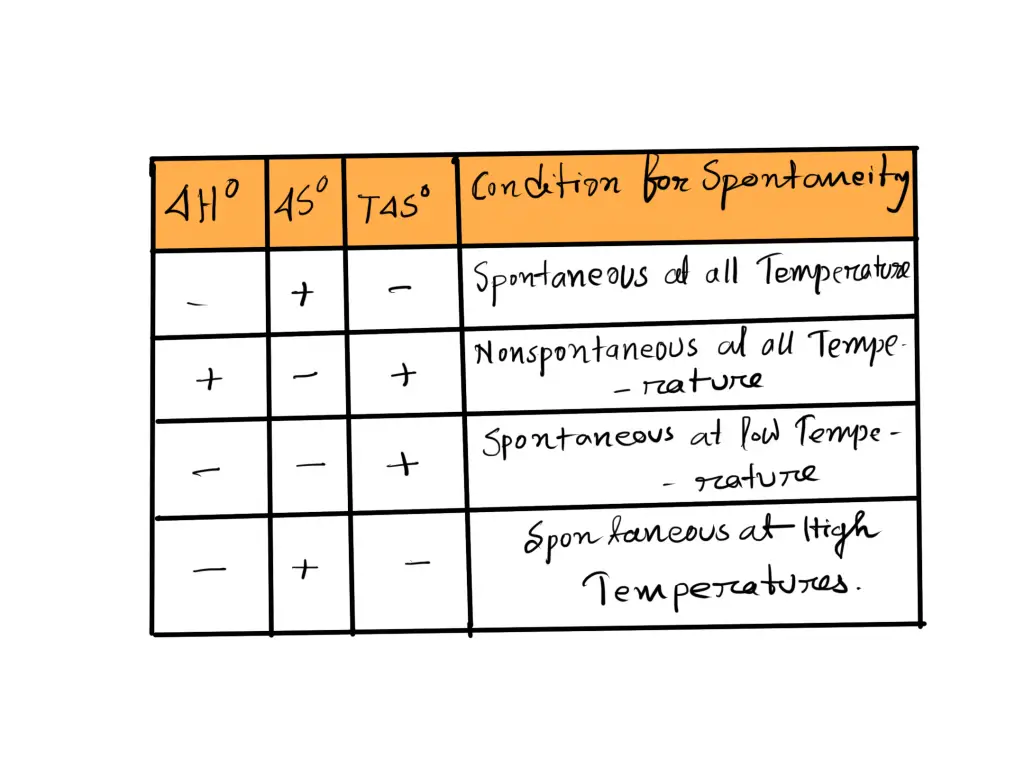
The following can be summarized about when a reaction is spontaneous.
If ΔH is Negative and ΔS is Positive
In the event that ΔH is negative, and ΔS are positive ΔG is always negative, and the reaction will be spontaneous at all temperatures.
If ΔH is Positive and ΔS is Negative
When ΔH is positive while ΔS is negative ΔG is never negative, and the reaction is not spontaneous at all temperatures. In fact, it could be said that reverse reactions happen spontaneously at all temperatures.
If ΔH and ΔS are Both Negative
In the event that ΔH both ΔS have negative polarities, ΔG will only be negative after a specific threshold temperature, and we can say that the reaction only occurs at low temperatures.’
If ΔH and ΔS are Both Positive
When ΔH both ΔS and ΔS have both been positive for a while, ΔG is only negative at a certain temperature. We say the reaction occurs only at high temperatures.’
The four options are presented in the following table:
The Relationship between ΔH and ΔS
There is a relation between ΔH and ΔS in a system at one of its temperatures that change phase, (i.e. the melting point or freezing temperature) students are usually expected to understand. Consider the boiling point of water that is 100oC. At this point you will have liquid and gaseous water at equilibrium with one another. For any system that is in equilibrium, ΔG=0 which leads to the following equation:
ΔG = ΔH – TΔS
0 = ΔH – TΔS
TΔS = ΔH
ΔS= ΔH/T
Delta S Delta H Relationship
It is from this last expression that undergraduate students are presented with equations that relate the freezing temperature to the ΔH and ΔS of fusion and the boiling temperature to the ΔH and ΔS of vaporization:

The equation in order to find the temperature, which may be employed to determine the freezing or boiling point. For reactions where ΔH as well as ΔS are either positive or negative, this formula can also be used to find the threshold temperature that is below the threshold at which reaction could be spontaneous.
One thing to bear in mind when performing calculations that involve the equations mentioned above is the fact that ΔG or ΔH values are usually expressed in kJ/mol, whereas ΔS values are usually listed in J/K.mol. Be sure to convert them to ensure that all units are equal (both J or both J…either way) prior to performing any calculations. Additionally, all temperatures must be expressed in Kelvin (the the absolute scale) in order to perform calculations.
Deriving the gibbs free energy formula
ΔG = ΔH – TΔS
We’ve had a look into Gibbs Free Energy as well as its relationship to changes in enthalpy as well as the change in the entropy of a reaction and how it can use to forecast the spontaneity of reactions But what exactly did Gibbs discover this? Although it’s not something that every student is required to learn, I’m putting it in this article to help the curious. Gibbs actually developed the equation for his newly invented “Gibbs Free Energy” specifically as a method to determine whether or not an event is spontaneous. He actually got this equation from 2nd Law of Thermodynamics which provides the following information:
For a spontaneous process the entropy change of the universe is positive.
We could also express the 2nd Law as follows:
For a spontaneous process, ΔSuniverse > 0
But there are two parts to the universe, the system and the surroundings, and we could express the 2nd Law one final time as follows:
For a spontaneous process, ΔSsystem + ΔSsurroudings > 0
This is where Gibbs started. But measuring quantities for the surroundings is problematic as it includes all the rest of the universe outside of the system being investigated. So Gibbs set out to devise a way to determine the spontaneity of a process based only upon thermodynamic properties of the system alone. For this he needed to define ΔSsurroundings in terms of the system and substitute it back into the 2nd Law. The change in entropy is defined as ΔS = qrev/T.
From this we can derive an expression for ΔSsurroundings:
ΔSsurroundings = ΔHsurroundings / T
However, the increase or decrease in the surrounding is caused by the flow of enthalpy into or from the system which is why ΔHsurroundings as well as ΔHsystem are the same in size however they are opposite in terms of sign: ΔHsurroundings = -ΔHsystem. We can substitute this into our definition of ΔSsurroundings.
ΔSsurroundings = ΔHsurroundings / T = -ΔHsystem / T
This can now be substituted back into the 2nd Law of Thermodynamics.
ΔSsystem + ΔSsurroudings > 0
ΔSsystem – ΔHsystem / T > 0
Finally multiplying all terms by -T yields Gibbs Free Energy equation (remember that multiplying or dividing an inequality by a negative number changes the sign).
-TΔSsystem + ΔHsystem < 0 rearranged ΔHsystem – TΔSsystem < 0
Gibbs now had a condition for spontaneity that relied only on thermodynamic properties of the system and then coined it ‘Gibbs Free Energy.’
ΔGsystem= ΔHsystem – TΔSsystem
And therefore we have derived from the 2nd Law of Thermodynamics:
For a spontaneous process, ΔHsystem – TΔSsystem < 0
For a spontaneous process, ΔGsystem < 0
And there you have it; Gibbs had devised a method of predicting if/when a process is spontaneous based upon thermodynamic properties of the system alone.
References
- https://www.chadsprep.com/chads-general-chemistry-videos/gibbs-free-energy/
- https://opentextbc.ca/introductorychemistry/chapter/gibbs-free-energy/
- https://chemistrytalk.org/what-is-gibbs-free-energy/
- https://www.chem.fsu.edu/chemlab/chm1046course/gibbs.html
- https://www.toppr.com/guides/chemistry/thermodynamics/gibbs-free-energy/
- https://www.thoughtco.com/definition-of-gibbs-free-energy-605869
- https://www.cliffsnotes.com/study-guides/chemistry/chemistry/thermodynamics/gibbs-free-energy
- https://www.chemguide.co.uk/physical/entropy/deltag.html
- https://www.corrosionpedia.com/definition/591/gibbs-free-energy-gfe
- https://en.wikipedia.org/wiki/Gibbs_free_energy
- https://www.khanacademy.org/science/chemistry/thermodynamics-chemistry/gibbs-free-energy/a/gibbs-free-energy-and-spontaneity
- https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Thermodynamics/Energies_and_Potentials/Free_Energy/Gibbs_(Free)_Energy
- https://chemed.chem.purdue.edu/genchem/topicreview/bp/ch21/gibbs.php


