Definition of p-value 

The p-value, or estimated probability represents the most reliable probability of providing the lowest amount of significance, that the null hypothesis isn’t the case.

• It is the ideal situation in which the results of the test are the same as the ones observed in reality with the assumption it is true that null hypotheses are true.
• A low p-value suggests that the possibility of the result, but not extremely likely in the absence of a null hypothesis.
• P-value is a substitute to the rejection point since they offer the lowest amount of significance that the null hypothesis cannot be valid.
• The P-value is the measure of significance of the statistical results of a hypothesis test.
• The main purpose that the value of p is to determine whether there’s enough evidence to disprove this null hypothesis.
• Since p-value is derived from other tests of statistical significance, including the t-test, the z score and the chi-score test, it is able to make a language universal for readers across the world.

Formula of p-value 

• P-values can be calculated by hand using the p-value tables or by using the use of spreadsheets, or software for statistical analysis.
• P-values are calculated based on the z-score, t score, or chi-square values derived from diverse tests.
• After the scores have been determined after which the scores are calculated, the results are utilized to determine the p-value of that particular score.
• There are tables with p-values for t-scores, z-scores, and chi-square that are used calculate the value of the scores.
• In spreadsheets, the P-value Formula Excel Template can be downloaded to Excel to calculate the p-values on the basis of the score as well as the degree of significance.

How to find p-value?

P-values can be determined through comparing test results against the table of p-values for various scores. The scores calculated by the test are then tallied on the tables in order to determine the P-values. In the event that the test is positive then the probability that is lower than the score is calculated using the value of the table containing p-values. The probability is then multiplied to calculate the value of the p-value. If the test statistic is positive, then the likelihood that is greater than the score of the test is calculated from the relevant value of the p-value table. This probability is then multiplied to obtain the score.

Table of p-value 

P-value tables differ for the various tests used to test hypothesis.

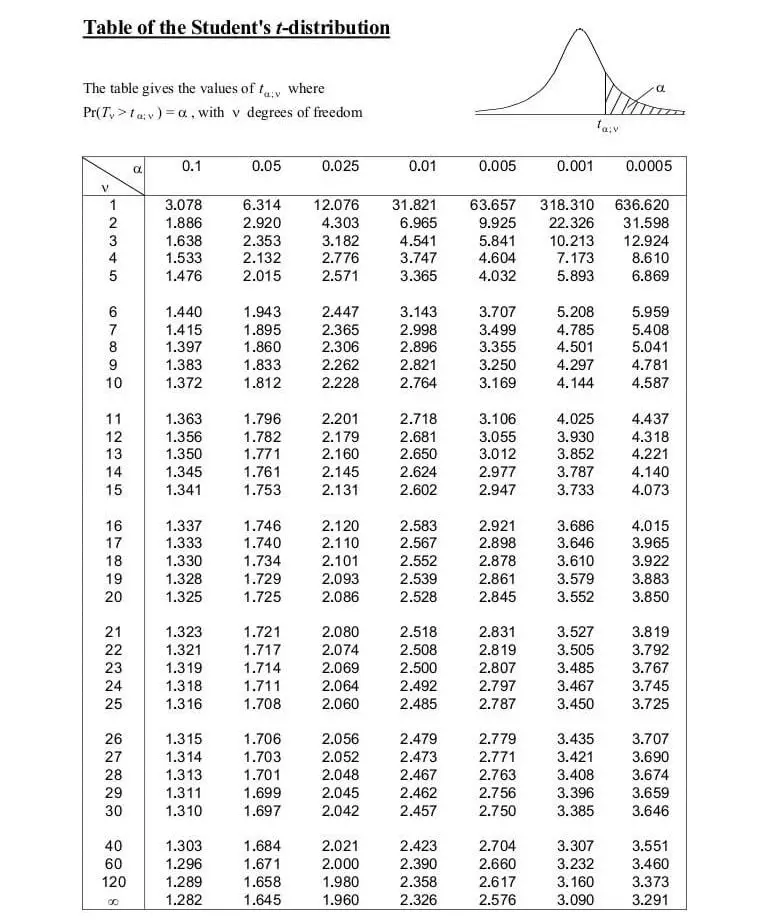
This table is the table for p-value to calculate the p-value based on the score of the t-score.

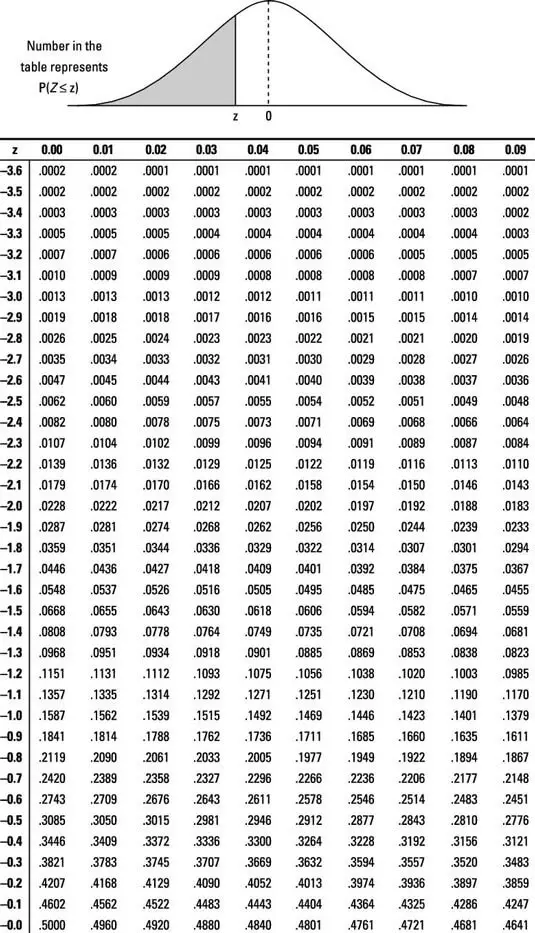
The table below contains the table for the p-value of z-score.

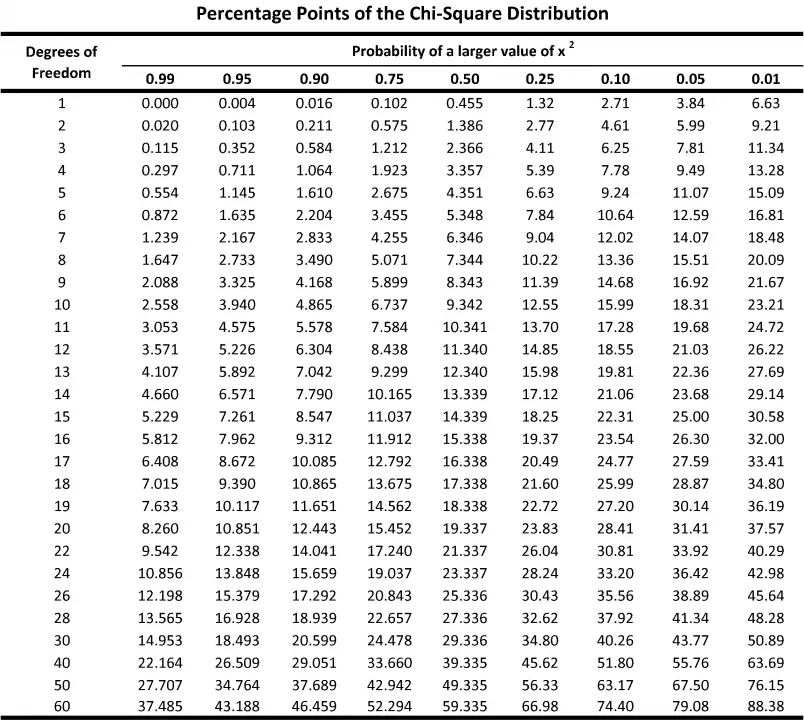
This table is the table of p-values for chi-squares.

Significance of p-value 

P-values are essential since they serve as an universal language for test results. Because different researchers apply differing levels of statistical significance when trying to test a hypothesis It can be challenging to assess the results from two tests. In such instances it is possible to determine p-values and used to determine the statistical significance of results. The hypothesis testing approach based on P-value testing utilizes probabilities to determine if there is sufficient evidence to disprove the hypothesis. P-value is regarded as an instrument to test whether the hypotheses are statistically significant. A p-value can be defined as a number in between 1 and 0, which is used in determining the significance of the result. The results can be used to interpret the results.

p-value less than 0.05

If the p-value is low (less than 0.05) is an evidence-based argument in support of the non-null hypothesis. In the end, it is decided to reject the hypothesis. Therefore, for a hypothesis that has an p-value lower than 0.05 The alternative hypothesis will be rejected while the alternate hypothesis gets accepted. This implies that the findings of the study/ research can be considered statistically relevant.

p-value greater than 0.05

When the value of p is high (greater than 0.05) is a sign of an insufficient evidence to support that null hypothesis. This means that the null hypothesis isn’t dismissed. So, for a hypotheses with an p-value higher than 0.05 The null hypothesis isn’t dismissed as the alternative hypothesis isn’t accepted. This implies that the findings of the study/research do not have statistical significance.

How to find p-value from t-test?

To find the p-value of the t-test beginning, the t test has required to be completed to get the t-score. Then , the level of freedom will be calculated by using d.f = (n-1) where the number n represents the amount of tests. When entering into the table using the degree of freedom that was calculated and then reading every row closest value to the t-score can be found. The probability of the value which is similar to the value found in the table is then written down. If it’s a one-tailed hypothesis, this value will be the p-value of the hypothesis.

If it is an inverse one then the probability value will be multiplied by the p-value to determine the value for the specific score. In addition, the p-value could be calculated from the t score on calculators for p-values.

How to find p-value from z-test?

To find the p-value obtained from the z-test, first, the z-test needs required to get the z-score. The z-score derived is calculated against the table in which it is the negative value of the 10th or hundredth position of the score are calculated against the column in the table while the one-th position is recorded on the row. For e.g. when the score 1.83, -1.8 is selected on the column. 1.83, -1.8 is selected on the column, while 0.03 is chosen on the row.

The value is determined by moving between the row and column using the Z-score. The result of the tally is then gathered as the value of the p-value. Additionally, the p value can be calculated using the z-score of calculators for p-values.

How to find the p-value from the chi-square test?

To determine the p-value derived from the chi square test, first the chi-square test needs required to get the chi-square score. When the test is being conducted, you will also need to determine the degree of freedom. is determined using the formula d.f = (c-1)(r-1) where c is the number of columns, and the r number is the number rows.

The distribution table for chi-squares is loaded, based on the degree of freedom that was calculated and the value of the chi square is recorded within the table. When the value cannot be determined, we select the range within which the chi-square value is located. The probability that corresponds to the values is chosen as the p-value. The p-value could be determined from the t-score of calculators for p-values.