Entropy is among the most important concepts that students should be able to comprehend clearly when learning Chemistry as well as Physics. In addition, entropy may be described in a variety of ways, which means it can be used in a variety of stages or scenarios, like the thermodynamics stage, in cosmic cosmology, or even in economics. The term “entropy” basically refers to the changes that occur spontaneously that take place in everyday phenomena as well as the general tendency to disorder.

Beyond being an academic term, entropy is typically described as a tangible physical property often related to uncertainty. However it’s also utilized in a variety of fields, ranging from classical thermodynamics to statistical Physics, and even Information Theory. Apart from its applications to Physics and Chemistry It is also used to biological systems and their connection to sociology, life and weather science, as well as climate change, as well as to determine the amount of transmission of information through the telecommunication industry.

Entropy Definition

Entropy can be defined as an index of disorder or randomness in the system. The concept was first invented by an German scientist by the name of Rudolf Clausius in the year 1850.

Beyond being the broad definition of it, there exist a variety of definitions, available to explain this concept. There are two different definitions to the term entropy we will examine on this page include the thermodynamic definition and the statistical definition.

From a thermodynamics perspective of Entropy, we do not examine the minute details of an entire system. Instead the term entropy is used to define the behavior of a system as a function of thermodynamic properties like pressure, temperature as well as entropy, temperature, and capacity. The thermodynamic explanation included the equilibrium state of the system.

In contrast, the definition of statistical that was created at a later time was based on thermodynamic properties that were defined using the statistics of the molecular movements of the system. Entropy is a measurement of molecular disorder.

Some other popular interpretations of entropy include;

• If we speak of quantum mechanics or quantum statistics, Von Neumann extended the notion of entropy into the quantum domain through the use using Density matrix.
• When discussing the theory of information, It is a measurement of the effectiveness of a system for transmitting signals, as well as the deficiency of data from the signal being transmitted.
• In the case of dynamic systems, entropy is the increasing complexity of an evolving system. It also measures the amount of information flow in a given amount of time.
• Sociology defines entropy as the natural decline in social structures or the decline of structures (such like law, organisation, or convention) within a social system.
• In cosmology, the term “entropy” is described as a potential possibility that the universe will achieve a maximum degree of homogeneity. It states that matter must be at an even temperature.

In any case, in the present, the term”entropy” is being used in a variety of other fields, far removed from physics or maths, and it is true that it is no longer able to maintain its strict quantitative nature.

Properties of Entropy

• Thermodynamic process.
• It is a state-related function. It is based on the condition of the system, and not the direction following.
• This is symbolized by S however, in the normal state it is represented as Sdeg.
• The SI units are J/Kmol.
• The CGS unit is the cal/Kmol.
• Entropy is an expansive property that means it grows according to the size of a system.

Note: The more disorder can be observed in a system that is not isolated and entropy will also increase. If chemical reactions take place, when reactants break down into more substances, the entropy is also raised. A system operating at higher temperatures has more randomness as compared to a system operating with a lower temperature. In these cases it is evident that entropy grows by decreasing the regularity.

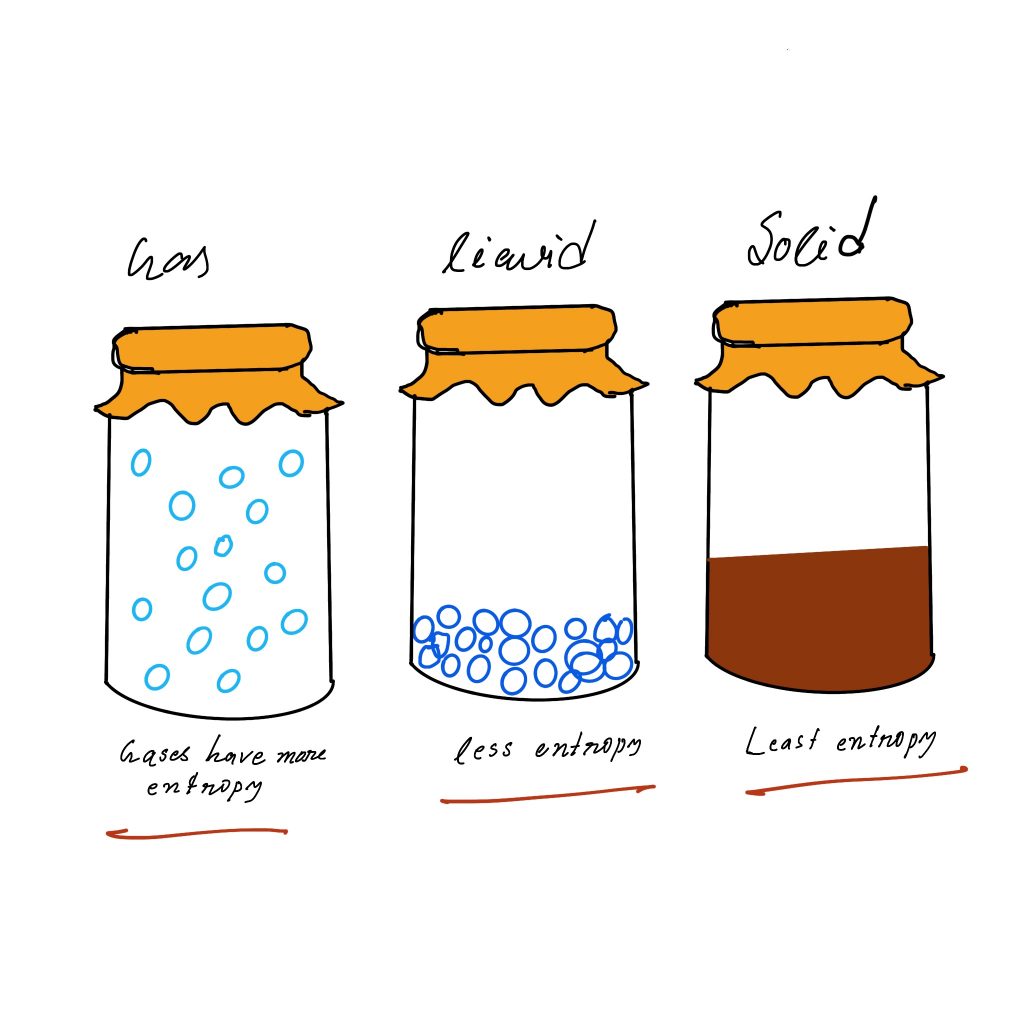
Entropy order: gas>liquid>solids

Entropy Equation and Calculation

There are many methods to calculate entropy but the two most popular equations refer to thermodynamic reversible processes as well as the isothermal (constant temperature) processes.

Entropy of a Reversible Process

Certain assumptions are in place when calculating the entropy for a reversible process. One of the most fundamental assumptions is that every configuration in the system is equal likely (which is not the case, but it could be). With equal probabilities of results, entropy is equal to Boltzmann’s constant (kB) multiplied by the natural logarithm of the number potential possibilities (W):

S = kB ln W

Boltzmann’s constant is 1.38065 × 10−23 J/K.

Entropy of an Isothermal Process

Calculus can be used to calculate an integral of the equation dQ/T that goes from the beginning state to the end state, where Q represents heat, and T represents the total (Kelvin) temp. of the system.

Another way of expressing this is to say that the change in the entropy (DS) is equal to the change in temperature (DQ) times the temperature absolute (T):

ΔS = ΔQ / T

Entropy and Internal Energy

In the field of thermodynamics and physical chemistry One of the most effective equations is that connects entropy with the inner energetics (U) of an entire system.

dU = T dS – p dV

The increase in the internal energy dU is equal to the absolute temperature T divided by change in entropy less external pressure p as well as the increase in the volume V.

Examples of Entropy

Here are some examples of Entropy:

• In a simple way think about the difference between a clean and a messy room. Clean rooms have very little energy. Each object is in its spot. A room that is messy and is high in the entropy. It takes energy to transform a messy room into a tidy one. It’s not like it does the cleaning.
• Dissolving can increase entropy. The solid changes from an orderly state to an unorganized one. For instance, mixing coffee with sugar increases the energy level of the system because sugar molecules are less well-organized.
• Osmosis and diffusion are both examples of entropy increasing. Molecules move naturally from areas with high concentrations to regions with lower concentrations until they are at equilibrium. As an example, if we spray fragrance in the corner of a room, you will eventually get a scent everywhere. However, once you’ve finished the scent doesn’t immediately go back to the bottle.
• Certain phase shifts between different states of matter provide an example of increasing entropy. others show a decrease in the amount of entropy. The ice-like block grows in entropy when it turns from a solid to liquid. It is composed of water molecules bound to one another in crystal lattice. When ice melts, molecules are able to gain energy, disperse further and lose structure, forming the liquid. In the same way, the transition from a liquid into a gas, such as that of steam to water, boosts the energy that the system produces. Condensing gas into an liquid or freezing a liquid to gas reduces the entropy in the matter. Molecules lose their kinetic energy and adopt an organized shape.

Entropy and Thermodynamics

This is where we examine or analyze the relation between entropy and different laws of thermodynamics.

First Law of Thermodynamics

It states that heat is a form of energy, and thermodynamic processes are therefore subject to the principle of conservation of energy. That means that heat energy can’t be made or destroyed. It is, however, able to be moved from one location to another, and then converted into or from other types of energy.

Note;

• Entropy increases as solid transforms to liquid and liquid transform into gas.
• Entropy can also increase when the amount of moles of gaseous substances exceeds the number of reactants.

Certain things are not in line with expectations regarding the entropy.

• An egg that has been hard-boiled is more the entropy of an egg that is not cooked. It is due to loss in the secondary form of albumin protein (albumin). Proteins change from the helical shape to the random form of a coiled.
• When we stretch a rubber band, the entropy decreases as macromolecules are uncoiled and put in a more orderly way. So, the probability of randomness is reduced.

Second Law of Thermodynamics

In accordance with the concepts of spontaneity and entropy The second law of thermodynamics can be described in many definitions.

• Naturally occurring spontaneous reactions are irreversible thermodynamically.
• Transformative transmission of heat to work is not thermodynamically feasible without the loss of an amount of energy
• The universe’s entropy is constantly growing
• Change in entropy total will always be positive. The entropy of the system as well as the entropy in its the surrounding environment will be greater than zero.

∆Stotal =∆Ssurroundings+∆Ssystem >0

Third Law of Thermodynamics

The entropy in any crystal is at its lowest as the temperature is close to the absolute temperature. This is due to the fact that it is possible to achieve a complete structure in the crystal when it is at absolute zero. The drawback of this rule is the fact that some crystals don’t have the zero entropy of absolute zero.

Example: glassy composed of a mix of isotopes.

Entropy Changes During Phase Transition

Entropy of Fusion

It’s the rise in entropy after solid melts and turns into liquid. The entropy rises when the mobility of molecules increases as changes in the phase.

The entropy of fusion is equal to the energy of fusion divided by the melting point(fusion temperature)

∆fusS=∆fusH / Tf

A natural process, such as a phase shift (eg. the fusion) occurs when the corresponding shift in Gibbs’ free energy is negative.

A majority of the time, the fusS is positive

A few exceptions: Helium-3 has an entropy that is negative for melting at temperatures less than 0.3 K. Helium-4 also has a slightly negative entropy of fusion when it is below 0.8 K.

Entropy of Vaporization

The entropy of vapourization is the state in which there is an increase in entropy due to the transformation of liquid into vapor. This is because of the increase in molecular motion which causes randomness of movement.

The entropy of vaporization is equivalent to the energy for the vaporization divided by the boiling point. It is represented by;

∆vapS=∆vapH / Tb

Standard Entropy of Formation of a Compound

It’s the change in entropy that occurs when one mole of a compound found in its standard state gets created by the elements present in the normal state.

Spontaneity

• Exothermic reactions occur spontaneously due to the fact that  ∆Ssurrounding is positive. This makes the ∆Stotal positive.
• Endothermic reactions occur spontaneously because ∆Ssystem is positive and ∆Ssurroundings is negative but overall ∆Stotal is positive.
• The criteria for free energy change to predict spontaneity are better than entropy-change criteria as the former only requires an energy exchange that is free and the latter demands an entropy shift of the environment and system.

Negentropy

It’s a reverse of the process of entropy. It refers to things becoming organized. “Order” means organization, structure and purpose. This is not the same as chaos or randomness. Negentropy is a good example. the star system, such as one in the solar system.

Entropy and Heat Death of the Universe

Certain scientists have predicted that the universe’s entropy will gradually increases until it becomes unusable to work. In the event that only thermal energy remains the universe is dead from heat death. But, some scientists disagree with the theory of heat death. Another theory considers the universe as a part of a larger structure.

Entropy and Time

Cosmologists and physicists frequently refer to the concept of entropy “the arch of the time” due to the fact that matter in isolated systems can shift between order and disorder. When you take a look at the Universe as it is, the amount of increasing entropy. As time passes, ordered systems are more disorganized and energy forms change eventually disappearing in the form of heat.

Factors Affecting Entropy

There are a myriad of elements that affect entropy. They can be summarized in the following manner:

1. Phase of Matter

The most important factor that influences Entropy is the phase of matter:

gas > liquid > solid

Solids are usually crystalline where the molecules, atoms and ions are placed in well-defined positions within an extremely ordered structure, resulting in a low energy loss.

Within the liquid phase molecules, atoms, and ions can freely move around, resulting in an increase of the variety of microstates, and an increase in entropy compared to the solid phase.

The gas phase is where molecules, atoms, and ions can be moved around, they are moving faster than in liquid and also have enormous growth in volume in comparison with the liquid phase. All of which leads to more possible microstates, and higher energy density. It is worth noting that there is a significant increase in energy entropy in the gas phase when opposed to the liquid or solid phase.

2. Higher Temperature, More Entropy

Higher temperatures translate to greater average energy kinetics. In the gas and liquid phases , molecules and atoms are moving more quickly, which results in a higher variety of possible microstates as well as more energy entropy. The solid phase, greater the kinetic energy will result in higher vibrations of the molecules/atoms/atoms within the crystal structure, which will also result in a larger number of microstates that could be possible and greater Entropy.

3. More Volume, More Entropy

A larger volume implies that there is a larger number of places for particles of the system to take up, which leads to an increased number of microstates that the system can experience and more Entropy. Because gases have a bigger volume than the liquid or solid which is why gases exhibit more entropy than either the solid or liquid.

4. More Particles, More Entropy

Entropy, it is discovered is an expansive property that is proportional to what size of the samples is. As the amount of particles present in a sample increase , so too do the possibilities of microstates that the system could be in, resulting in an increase in amount of entropy.

What is ΔS?

ΔS, which is the variation in entropy, is typically determined by the amount of heat transferred by an irreversible process multiplied by the temperature where the process was executed.

ΔS = q_rev⁄ T

A reversible process is one carried out under equilibrium conditions.

The term “enthalpy” is used to describe being the same as the heat transfered at the same pressure.

ΔH = q_P

Substituting this into the above expression would lead us to a relationship between ΔS and ΔH for phase changes:

ΔS^o_fus = ΔH^o_fus ⁄ T_m                ΔS^o_vap = ΔH^o_vap ⁄ T_b

ΔS of a reaction can also be calculated from absolute entropies:

ΔS^o_rxn = ΣnS^o_products – ΣmS^o_reactants

How to Predict the Sign of ΔS

Three important aspects are needed to consider when determining the signs of ΔS:

1. An alteration in Moles of Gas

Gases are significantly more entropy than solids or liquids. The most popular method of predicting the presence of ΔS is to detect an increase in the number moles of gas:

A rise in the mole count of gas is correlated with an increase in the entropy (ΔS > 0).

2C(s, graphite) + O2(g) → 2CO(g)    ΔS^o = +179 J/K

An increase in amount of gas molecules is correlated with the decrease in the entropy (ΔS < 0).

2H2(g) + O2(g) → 2H2O(g)    ΔS^o = -88.5 J/K

A reaction that does not change in moles of gas will likely have an ΔS  value of a small magnitude. It could be positive or negative, however it most likely, it will be near zero in either case.

N2(g) + O2(g) → 2NO(g)    ΔS^o = +25 J/K  (closer to zero than the previous examples)

2. Phase Changes

Since the matter’s phase can have a major impact on the rate of entropy, it is a predictable process (gas > liquid > solid) it should be no surprise that it is relatively straightforward to predict ΔS for a phase change.

ΔS is positive for fusion, vaporization and sublimation.

ΔS is negative for freezing, condensation, and deposition.

These are summarized below:

3. A Change in Complexity of the Substances

If there isn’t any variation in the amount of moles in gas and the reaction isn’t just an alteration in the phase, or a change in the nature of the substance could enable you to determine the manifestation of ΔS.

An increase in complexity will result in the creation of a positive ΔS, and an increase in complexity will result in negative ΔS.

The change in complexity is caused by the presence of more atoms or elements. For instance, consider one reaction which was utilized as an earlier illustration of when there was an absence of change to the quantity of moles in gas:

N2(g) + O2(g) → 2NO(g)    ΔSo = +25 J/K

There are two gas molecules on the reactionants’ side as well as on the products’ side, so there isn’t a changes in the moles of gas. It is also impossible to define this as a phase shift as well. We’re left with a discussion of the complexity.

All the components used with this chemical reaction have diatomic. However, the reactants, N2 and O2 are both symmetrical, being made up of two identical atoms however, the product, NO, are not as symmetrical because they are composed of two different molecules. The reaction products that are symmetrical have a lesser amount of degree of freedom that we consider to be a sign of their complexity. We could, in the end, rotate 180 degrees and not discern the difference due to the symmetry. However, if you were to rotate zero-molecular 180deg, you will certainly detect the distinction. This complexity increase is the reason for why there is a (slightly) positive result for ΔS.

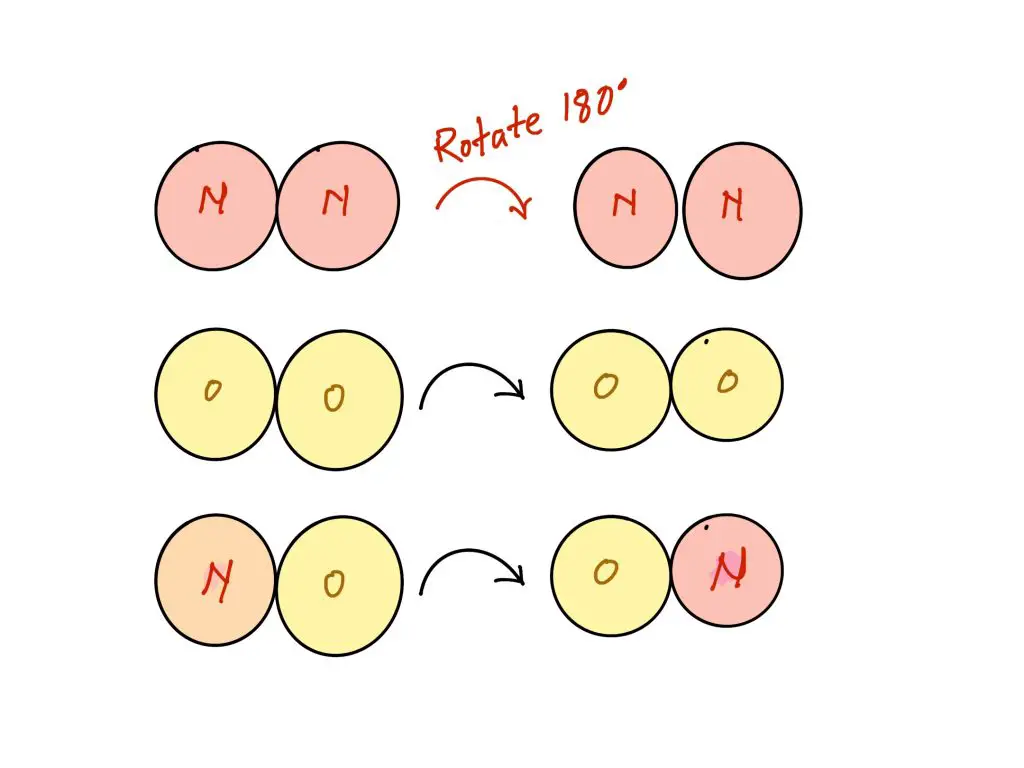
The two conformations of rotation can be distinguished from the other for NO, however neither for O2 nor N2. This suggests that there are a larger number of microstates possible for NO molecules. This is why more complexity is likely to lead to higher entropy.

References

• Atkins, Peter; Julio De Paula (2006). Physical Chemistry (8th ed.). Oxford University Press. ISBN 978-0-19-870072-2.
• Watson, J.R.; Carson, E.M. (May 2002). “Undergraduate students’ understandings of entropy and Gibbs free energy.” University Chemistry Education. 6 (1): 4. ISSN 1369-5614
• Clausius, Rudolf (1850). On the Motive Power of Heat, and on the Laws which can be deduced from it for the Theory of Heat. Poggendorff’s Annalen der Physick, LXXIX (Dover Reprint). ISBN 978-0-486-59065-3.
• Chang, Raymond (1998). Chemistry (6th ed.). New York: McGraw Hill. ISBN 978-0-07-115221-1.
• Landsberg, P.T. (1984). “Can Entropy and “Order” Increase Together?”. Physics Letters. 102A (4): 171–173. doi:10.1016/0375-9601(84)90934-4
• http://hyperphysics.phy-astr.gsu.edu/hbase/Therm/entrop.html
• https://www.priyamstudycentre.com/2020/04/entropy.html
• https://www.thoughtco.com/definition-of-entropy-604458
• https://lawofthermodynamicsinfo.com/definition-of-entropy-in-thermodynamics/
• https://www.chadsprep.com/chads-general-chemistry-videos/entropy-delta-s/
• https://byjus.com/jee/entropy/