What is Michaelis–Menten model?

The Michaelis–Menten model is a fundamental concept in biochemistry, specifically in the realm of enzyme kinetics. Enzymes, which are proteins, play a pivotal role as catalysts in biochemical reactions. Their primary function is to reduce the Gibbs free energy of activation, ΔG, thereby facilitating the reaction to reach its transition state more efficiently.

The rate of many enzyme-catalyzed reactions, represented as v, can be described using the Michaelis–Menten equation. This equation is particularly applicable to reactions involving one substrate and one product. The relationship between the velocity and substrate concentration in enzymes exhibiting Michaelis–Menten kinetics is hyperbolic in nature.

Named after Leonor Michaelis and Maud Menten, the Michaelis–Menten kinetics is the most basic form of enzyme kinetics. The equation is given by:

\( v = \frac{d[p]}{dt} = \frac{Va}{K_m + a} \)

In this equation, V or often represented as Vmax​, signifies the maximum rate achieved by the system when the substrate concentration is at saturation for a given enzyme concentration. The Michaelis constant, denoted as Km​, is a significant parameter. When the substrate concentration is numerically equal to Km​, the reaction rate is half of V.

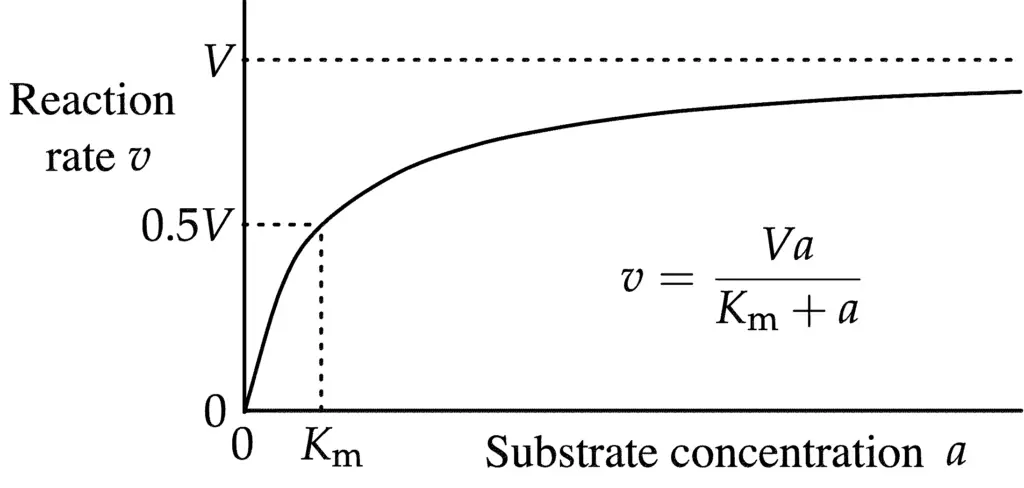
It’s essential to note that while many biochemical reactions involving a single substrate are often assumed to adhere to Michaelis–Menten kinetics, this assumption is made without always considering the foundational assumptions of the model. Although only a minor fraction of enzyme-catalyzed reactions involve just one substrate, the equation remains applicable if only one substrate concentration is altered.

Therefore, the Michaelis–Menten model provides a detailed and sequential explanation of enzyme kinetics. Besides its technical vocabulary, the model emphasizes the functions of various components, ensuring a clear, concise, and objective understanding of the topic.

Michaelis–Menten plot

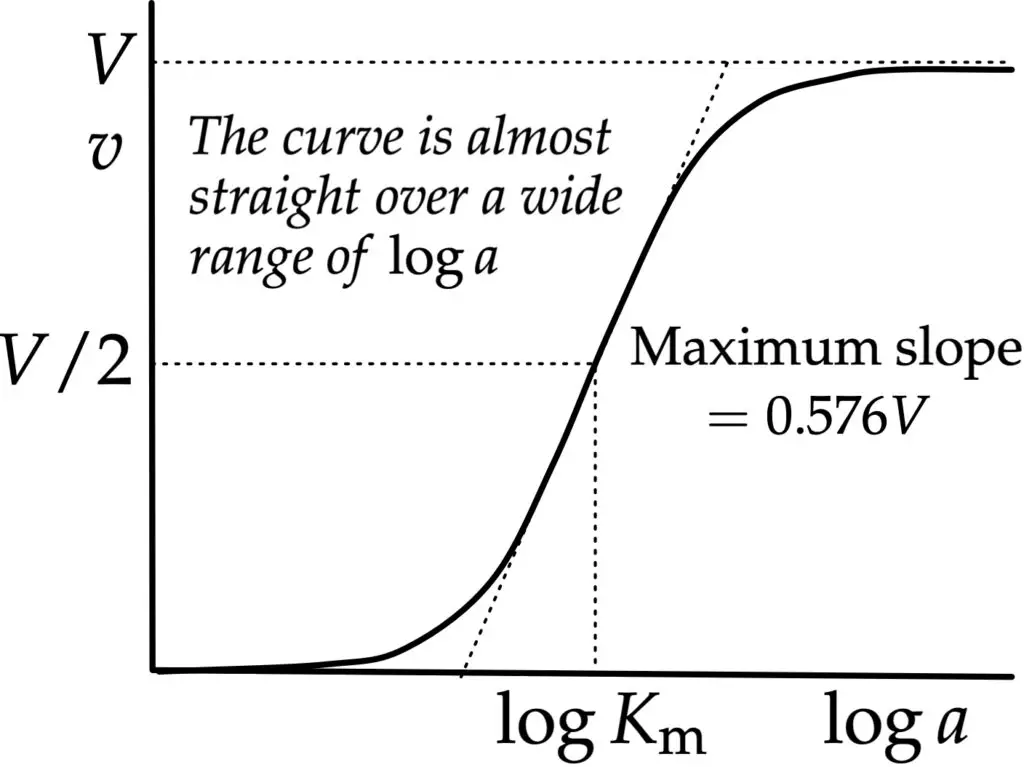
The Michaelis–Menten plot is a graphical representation used in enzyme kinetics. Contrary to popular belief, the traditional plot of v against a is not what Michaelis and Menten originally used. Instead, they opted for a plot of v against loga. This approach offers several advantages over the conventional methods of plotting Michaelis–Menten data.

Firstly, by having v as the dependent variable, the plot does not distort the experimental errors in v. This ensures a more accurate representation of the data. Michaelis and Menten did not aim to estimate V directly from the limit approached at high log⁡loga. Given the limitations of their data and the challenges associated with modern techniques, such an estimation would have been challenging. Therefore, they leveraged the fact that the curve is nearly linear in the middle range and has a maximum slope of 0.576V, which is equivalent to 0.25ln10⋅V. With an accurate value of V, it became straightforward to determine logKm​ from the point on the curve corresponding to 0.5V.

However, in contemporary times, this specific plot is seldom used for estimating V and Km​. But its significance remains intact, especially when comparing the properties of isoenzymes that catalyze the same reaction but are active in vastly different substrate concentration ranges. For instance, the four mammalian isoenzymes of hexokinase exhibit half-saturation by glucose at concentrations that vary greatly. The range spans from approximately 0.02 mM for hexokinase A (brain hexokinase) to about 50 mM for hexokinase D (also known as “glucokinase” or liver hexokinase), representing a variation of over 2000-fold. A conventional plot would fail to provide a clear kinetic comparison between these isoenzymes. However, a semi-logarithmic plot effectively captures this wide range of data, making it invaluable for such comparisons.

In conclusion, the Michaelis–Menten plot, specifically the loga variant, offers a detailed and sequential explanation of enzyme kinetics. It emphasizes the functions of various components, ensuring a clear, concise, and objective understanding of the topic. The use of technical vocabulary, transitional phrases, and a consistent third-person point of view further enhances the clarity and objectivity of the content.

The Michaelis–Menten model

\( E + S \underset{k_2}{\overset{k_1}{\rightleftharpoons}} ES \overset{k_3}{\rightarrow} E + P \)

The Michaelis–Menten model is a foundational concept in the field of enzyme kinetics. Named after its developers, German biochemist Leonor Michaelis and Canadian physician Maud Menten, this model provides a mathematical description of the rate at which enzymatic reactions occur. Specifically, it relates the reaction rate v (which represents the rate of formation of the product [P]) to the concentration of a substrate [S].

Delving deeper into the model, it is based on the principle of enzyme catalysis. Here’s a detailed and sequential explanation of the process:

1. Initially, the enzyme (E) interacts with its substrate (S), leading to the formation of an enzyme–substrate complex, denoted as (ES).
2. This (ES) complex can then undergo two potential pathways. It can either dissociate back into its original constituents, E and S, or it can undergo a chemical transformation to produce the enzyme (E) and the product (P).
3. The progression of these steps is governed by rate constants: k1, k2, and k3. Each of these constants represents the rate associated with each specific step of the catalytic process.
4. An essential assumption of the Michaelis–Menten model is that there’s no significant backward reaction where the enzyme and product (E + P) revert to the ES complex.
5. Another crucial aspect is that the concentration of the [ES] complex remains relatively constant throughout most of the reaction. This means that the rate of formation of the ES complex is roughly equal to its rate of consumption, leading to a steady state of [ES].

Therefore, based on these principles, the Michaelis–Menten equation was formulated. This equation serves as a cornerstone in biochemistry, offering insights into the intricate dynamics of enzymatic reactions. Besides its theoretical significance, the model also provides a framework for understanding how enzymes function and how they can be influenced by various factors. In essence, the Michaelis–Menten model emphasizes the functions and interactions of enzymes and substrates, presenting the information in a clear, concise, and objective manner, enriched with technical biological terms.

The Michaelis–Menten equation

\( V_0 = \frac{V_{\text{max}} \times [S]}{K_m + [S]} \)

The Michaelis–Menten equation is a fundamental equation in the realm of enzyme kinetics, providing a mathematical representation of the relationship between the rate of an enzymatic reaction and substrate concentration. Here’s a detailed exposition of the equation and its components:

1. Michaelis Constant (Km): This constant is defined as (k2+k3)/k1. It represents the affinity of an enzyme for its substrate. Specifically, Km is the substrate concentration at which the reaction velocity is half of its maximum value (Vmax). The lower the value of Km, the higher the enzyme’s affinity for its substrate. Therefore, Km is a measure of how easily the enzyme can be saturated by the substrate.
2. Maximum Velocity (Vmax): This is the maximum rate of the enzymatic reaction. It is achieved when all the enzyme molecules are bound to the substrate, forming the enzyme–substrate complex. In other words, Vmax is reached when the entire enzyme is in the enzyme–substrate complex form.
3. Rate of Product Formation: The velocity (v) of the reaction, which denotes the rate of product formation, is directly proportional to the concentration of the enzyme–substrate complex. Mathematically, this relationship is represented as: v=k3[ES] Where k3 is the rate constant for the conversion of the enzyme–substrate complex to the enzyme and product.
4. Relation to Substrate Concentration: When the substrate concentration (S) is equal to Km, the velocity of the reaction is half of its maximum value. Substituting Km for S in the Michaelis–Menten equation results in: v=1/2Vmax This relationship emphasizes that Km is the substrate concentration at which the reaction velocity is 50% of Vmax.
5. Graphical Representation: When the reaction velocity (v) is plotted against substrate concentration (S), the resulting graph produces a hyperbolic curve. This curve is characteristic of many enzymatic reactions and provides insights into the enzyme’s efficiency and substrate affinity.

In conclusion, the Michaelis–Menten equation offers a comprehensive understanding of enzyme kinetics. It emphasizes the functions of enzymes in catalyzing reactions and their interactions with substrates. The equation, with its technical vocabulary and descriptive details, provides a clear, concise, and objective overview of the topic, ensuring a smooth flow of ideas and logical progression.

What is Enzyme velocity?

Enzyme velocity, in the realm of biochemistry, refers to the rate at which an enzyme-catalyzed reaction occurs. Here’s a detailed exposition on the concept:

1. Definition: Enzyme velocity is commonly termed as the speed or rate of an enzyme-catalyzed reaction. It provides insights into how efficiently an enzyme can facilitate the transformation of a substrate into a product.
2. Initial Velocity (Vo): Enzyme velocities are typically measured and reported as initial velocities, denoted by the symbol Vo. This velocity is measured in terms of micromoles per minute (μmol min-1). The emphasis on initial velocity arises because the reaction rate is at its peak when no product has been formed yet.
3. Importance of Time Zero: The rationale behind focusing on the initial velocity is that the substrate concentration is at its maximum before any of it has been converted into the product. Therefore, the reaction’s rate is fastest at this point, providing a clear indication of the enzyme’s efficiency under optimal conditions.
4. Graphical Representation: When plotting the amount of product formed against time for an enzyme-catalyzed reaction, a distinct pattern emerges. Initially, there’s a rapid formation of the product, resulting in a linear portion on the graph. This rapid phase signifies the highest enzyme activity. However, as the reaction progresses, there’s a noticeable decline in the rate. This deceleration can be attributed to the depletion of the substrate and/or potential loss of enzyme activity over time.
5. Determining V0: To ascertain the initial velocity (V0), one must focus on the linear segment of the product formation curve. By drawing a straight line through this linear part, starting from the zero time-point, the slope of this line provides the value of V0. This slope represents the maximum rate of product formation when the enzyme is most active.

Substrate and enzyme concentration

Substrate and enzyme concentrations play a pivotal role in determining the rate of enzyme-catalyzed reactions. Here’s an expository breakdown of their relationship and significance:

1. Initial Relationship: At the outset, when substrate concentrations ([S]) are low, the relationship between the substrate concentration and the initial velocity (V0) of the reaction is directly proportional. This means that if the substrate concentration is doubled, the initial velocity of the reaction will also double. This phase represents the initial stages where the enzyme has ample opportunity to interact with the substrate.
2. Saturation Point: As substrate concentrations continue to increase, a point is reached where the enzyme becomes saturated. Beyond this point, even if the substrate concentration is further increased, there will only be negligible changes in V0. This phenomenon occurs because, at these high substrate concentrations, all enzyme molecules are occupied with the substrate, leaving no free enzyme molecules to facilitate further reactions.
3. Enzyme Rate Dependency: When the enzyme is saturated with the substrate, the rate of the enzyme-catalyzed reaction becomes dependent on how quickly the product can dissociate from the enzyme. Adding more substrate at this stage will not influence this rate, as the enzyme is already operating at its maximum capacity. Graphically, when V0 is plotted against [S], the resulting curve is hyperbolic in nature, reflecting the saturation effect.
4. Enzyme Concentration Impact: In scenarios where the substrate concentration is so high that it saturates the enzyme, the enzyme concentration becomes the determining factor for the reaction rate. In such cases, if the enzyme concentration is doubled, V0 will also double. This direct relationship results in a linear graph when V0 is plotted against the enzyme concentration.

What is Michaelis-Menten Constant?

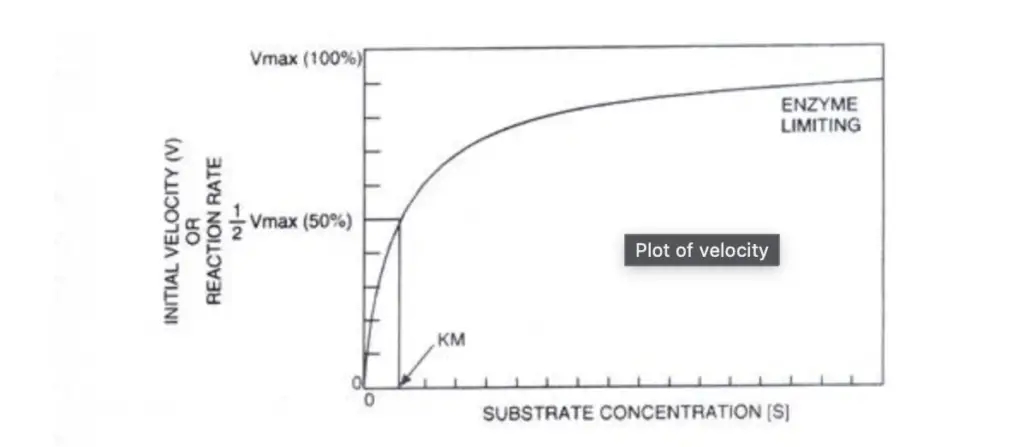
In the realm of enzyme kinetics, understanding the relationship between substrate concentration and reaction rate is pivotal. The Michaelis-Menten Constant, commonly denoted as Km, plays a crucial role in this understanding. This expository piece aims to elucidate the concept of the Michaelis-Menten Constant, emphasizing its functions and significance in enzyme-substrate interactions.

When observing an enzyme-catalyzed reaction, especially when there’s an abundance of substrate and a constant enzyme concentration, a specific pattern emerges. Plotting substrate concentration (S) against the velocity (V) or reaction rate yields a hyperbolic curve, often referred to as a saturation plot. Initially, as substrate concentration increases, the reaction rate also increases proportionally. However, a point is reached where the reaction rate plateaus. At this juncture, adding more substrate doesn’t enhance the reaction rate. This plateau occurs because all the enzyme’s active sites are saturated with substrate molecules. Therefore, any further increase in reaction rate necessitates the addition of more enzyme.

Central to this discussion is the Michaelis-Menten Constant (Km). This constant represents the substrate concentration required to achieve half of the maximum reaction rate (1/2​Vmax​). Essentially, Km reflects the affinity of an enzyme for its substrate and is a defining characteristic of a specific enzyme-substrate system. A smaller Km value indicates a stronger binding affinity between the enzyme and its substrate. It’s noteworthy that enzymes catalyzing reactions involving multiple substrates will exhibit distinct Km values for each substrate.

The relationship between substrate concentration, reaction rate, and the Michaelis-Menten Constant is encapsulated in the Henri-Michaelis-Menten equation:

V = V_max[S]/Km+ [S]

In this equation:

• V denotes the velocity or reaction rate.
• Vmax​ signifies the maximum reaction rate achievable at infinite substrate concentration.
• S represents the substrate concentration.
• Km is the Michaelis constant.

It’s imperative to note that while Km values are relatively constant for specific enzyme-substrate pairs, they can exhibit minor variations based on factors like pH, temperature, and ionic strength. Additionally, the presence and quantity of coenzymes, if required for the reaction, can also influence Km values. Typically, Km values for many enzymes fall within the range of 10⁻³ to 10⁻⁶ molar (1mM – 1 µM).

In conclusion, the Michaelis-Menten Constant offers invaluable insights into enzyme-substrate interactions, shedding light on the enzyme’s affinity for its substrate. By maintaining an objective tone, using technical vocabulary, and providing a detailed and sequential explanation, this exposition aims to offer a clear and concise understanding of the Michaelis-Menten Constant and its significance in enzyme kinetics.

Significance of Michaelis-Menten Constant

The Michaelis-Menten Constant, commonly represented as Km, is a pivotal parameter in enzyme kinetics. It provides valuable insights into the intricate dynamics between enzymes and their respective substrates. Here, we delve into the significance of the Michaelis-Menten Constant, elucidating its role and importance in the realm of biochemical reactions.

1. Indicator of Enzyme-Substrate Affinity: The Km value is a reflection of the affinity of an enzyme for its substrate. Specifically, it denotes the substrate concentration at which the reaction velocity is half of its maximum value, Vmax​. A lower Km value implies a higher affinity of the enzyme for its substrate, meaning the enzyme can bind to its substrate even at low concentrations. Conversely, a higher Km suggests a lower affinity.
2. Predictor of Cellular Needs: Understanding the Km value of a specific enzyme-substrate system allows one to anticipate the cellular requirements to optimize the enzymatic reaction. If the reaction rate needs to be accelerated, the cell can either produce more enzyme or increase the substrate concentration, depending on the Km value.
3. Preference for Multiple Substrates: In scenarios where an enzyme can catalyze reactions with multiple similar substrates, the enzyme will exhibit a preference for the substrate with which it has a lower Km value. This is because the enzyme binds more readily and efficiently to that particular substrate.
4. Estimation of Substrate Concentration: The Km value offers an approximate measure of the substrate concentration in the specific cellular region where the enzymatic reaction takes place. Enzymes that catalyze reactions with substrates present in higher concentrations typically have a higher Km value. In contrast, enzymes interacting with substrates in low concentrations, such as hormones, tend to have a lower Km value.
5. Insight into Enzymatic Efficiency: The Km value, when considered alongside other kinetic parameters like Vmax​ and the turnover number, provides a comprehensive view of the efficiency of an enzyme. An enzyme with a low Km and high Vmax​ is considered highly efficient.

In conclusion, the Michaelis-Menten Constant is not just a numerical value; it is a profound indicator of the dynamics of enzyme-substrate interactions. It plays a crucial role in understanding and predicting the behavior of enzymes in various biochemical

Importance of The Michaelis–Menten equation

Here, we explore the importance of the Michaelis–Menten equation in the realm of biochemistry and its broader implications:

1. Descriptive Power: The Michaelis–Menten equation, given by V=Km​+[S]Vmax​[S]​, describes the rate of enzymatic reactions as a function of substrate concentration. It elegantly captures the relationship between reaction velocity (V), maximum reaction velocity (Vmax​), substrate concentration ([S]), and the Michaelis constant (Km​).
2. Enzyme Saturation Insight: The equation elucidates the concept of enzyme saturation. As substrate concentration increases, the reaction velocity approaches its maximum value, Vmax​, indicating that all enzyme active sites are occupied by substrate molecules.
3. Determination of Enzyme Affinity: The Michaelis constant, Km​, derived from the equation, is a measure of the substrate concentration at which the reaction rate is half of Vmax​. It provides insights into the affinity of the enzyme for its substrate, with a lower Km​ indicating higher affinity.
4. Basis for Enzyme Inhibition Studies: The Michaelis–Menten equation serves as a foundation for understanding enzyme inhibition mechanisms. By studying deviations from typical Michaelis–Menten kinetics, researchers can identify and characterize various types of enzyme inhibitors, essential for drug development.
5. Predictive Utility: The equation allows biochemists to predict how changes in substrate concentration will impact the rate of enzymatic reactions. This predictive power is crucial for designing experiments and optimizing conditions in both research and industrial settings.
6. Framework for Further Models: The Michaelis–Menten equation has paved the way for the development of more complex kinetic models. These models account for multi-substrate reactions, allosteric effects, and other intricate biochemical phenomena.
7. Clinical and Pharmaceutical Applications: Understanding enzyme kinetics through the Michaelis–Menten equation is vital in the medical and pharmaceutical fields. It aids in drug design, understanding drug interactions, and predicting the behavior of enzymes under various conditions.
8. Educational Value: The Michaelis–Menten equation is a cornerstone in biochemistry education. It provides students with a tangible mathematical framework to understand the abstract concepts of enzyme function and kinetics.